En los casos en los que nuestra variable dependiente no esté expresada sólo en términos de la variable independiente, se tiene una función implícita. Una expresión equivalente a  es
es  . Esta expresión no nos presenta a y en términos de x, por lo que en este caso tenemos a la función definida de manera implícita.
. Esta expresión no nos presenta a y en términos de x, por lo que en este caso tenemos a la función definida de manera implícita.
viernes, 22 de noviembre de 2013
FUNCIONES IMPLICITAS
Las funciones pueden clasificarse en funciones explícitas e implícitas. Una función en la que la variable dependiente se expresa ÚNICAMENTE en términos de la variable independiente es una función explícita. La forma de estas funciones es y = f(x), y al derivarlas, la idea es encontrar y’. Por ejemplo, la función  es una función explícita.
es una función explícita.
REGLA DE LOS 4 PASOS
DERIVADA POR LOS CUATRO PASOS
Para encontrar la derivada de una función se utiliza la Regla General para la Derivación que consta de cuatro pasos:
Primer paso.- Se sustituye en la función “X” por (X + ΔX), y “Y” por (Y + ΔY).
Segundo paso.- Se resta a la nueva función el valor de la función original, obteniendo únicamente Δy ( incremento de la función ).
Tercer paso.- Se divide la nueva ecuación Δy (incremento de la función ) entre Δx ( incremento de la variable independiente).
Cuarto paso.- Se calcula el límite cuando Δx (incremento de la variable independiente ) tiende a cero.
La regla general se puede representar a través de la siguiente ecuación:
EJEMPLOS DE RESOLUCION DE LA DERIVADA CON LA REGLA GENERAL

SIMBOLOGIA DE LA DERIVADA
El concepto de derivada fue desarrollado por Leibniz y Newton. Leibniz fue el primero en publicar la teoría, pero parece ser que Newton tenía papeles escritos (sin publicar) anteriores a Leibniz.
Simbolos:
El símbolo f´(x), para las derivadas, fue introducido por Lagrange en 1797 en Théorie des fonctions analytiques.
Newton usó el apóstrofo para representar la derivada de una función. Así, para la función f(x) se representa su derivada como la función f'(x).
Newton usó el apóstrofo para representar la derivada de una función. Así, para la función f(x) se representa su derivada como la función f'(x).
Leibniz en cambio usó una delta minúscula de la función (usada a veces como una d latina) siempre haciendo referencia a la variable respecto a la cual se deriva.Así la derivada de y respecto a x es dy/dx
En símbolos, sea y = f(x), entonces la derivada de “y” con respecto a “x” es:
dy
y
y´ = = f´(x) = fx (x) = Lim
dx
!x
x
dy
y
y´ = = f´(x) = fx (x) = Lim
dx
!x
x
Los símbolos dx, dy y dx/dy, para las derivadas, fueron introducidos por Leibniz.Los símbolos f´(x), f´´(x), etc. para las derivadas, fueron introducidos por Lagrange en 1797 en Théorie des fonctions analytiques.El símbolo d para la derivada parcial fue usada en 1770 por Antoine-Nicolas Caritat, marques de Condorcet en Memoire sur les Equations aux différence partielles. Jacobi usó este símbolo extensamente, por ello se le suele llamar la delta de Jacobi.
RECTA TANGENTE
Pendiente
La pendiente de la recta tangente a una curva en un punto
es la derivada de la función en dicho punto.

Ecuación de la recta tangente
La recta tangente a a una curva en un punto es aquella
que pasa por el punto (a, f(a)) y cuya pendiente es igual a f '(a).
DEFINICION DE DERIVDA
La derivada es uno de los conceptos más importante en matemáticas. La derivada es el resultado de un límite y representa la pendiente de la recta tangente a la gráfica de la función en un punto. Pero vayamos por partes.
La definición de derivada es la siguiente:
Podría, pues, no existir tal límite y ser la función no derivable en ese punto. En esta primera práctica vamos a ver qué significa cada uno de los términos que aparecen en la formula anterior.
miércoles, 13 de noviembre de 2013
lunes, 28 de octubre de 2013
PROPIEDADES DE LOS LIMITES.
LIMITE DE UNA CONSTANTE
LIMITE DE UNA SUMA
LIMITE DE UN PRODUCTO
LIMITE DE UN COCIENTE

LIMITE DE UNA POTENCIA
LIMITE DE UNA FUNCION
g puede ser una raíz, un log, sen ,cos, tg, etc.
LIMITE DE UNA RAIZ
LIMITE DE UN LOGARITMO
LIMITES INFINITOS Y SUS PROPIEDADES.
Observemos la función f(x)=1/x2 para valores de x positivos muy grandes.
| x | f(x) |
|---|---|
| 100 | 1,0x10-4 |
| 1.000 | 1,0x10-6 |
| 10.000 | 1,0x10-8 |
| 100.000 | 1,0x10-10 |
| 1.000.000 | 1,0x10-12 |
Si tomamos x cada vez mayor, f(x) está cada vez más cerca de 0. Si x es suficientemente grande podemos conseguir que f(x) se acerque a 0 tanto como queramos. Decimos que f(x) tiende a 0 cuando x tiende a infinito.
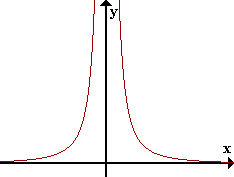
Veamos a continuación las definiciones precisas de cada uno de los límites que involucran al infinito.
PROPIEDADES.
Caso 1:
limx->af(x) = +inf <=> para todo A > 0 existe δ > 0 / para todo x perteneciente al E*a,δ f(x) > A .
El límite de f(x) cuando x->a es infinito positivo, si para cualquier número positivo A (tan grande como se quiera), podemos encontrar un número δ tal que, para todos los x dentro del entorno reducido de a de radio δ se cumple que f(x) es mayor que A.
En otras palabras, si para cualquier número positivo A que consideremos, existe un entorno reducido de a donde la función vale más que A, quiere decir que f(x) puede hacerse mayor que cualquier número, con tal de que x se acerque lo suficiente a a. Por eso se dice que el límite de f(x) cuando x tiende a a es +inf.
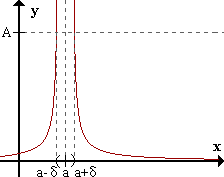
limx->af(x) = +inf <=> para todo A > 0 existe δ > 0 / para todo x perteneciente al E*a,δ f(x) > A .
El límite de f(x) cuando x->a es infinito positivo, si para cualquier número positivo A (tan grande como se quiera), podemos encontrar un número δ tal que, para todos los x dentro del entorno reducido de a de radio δ se cumple que f(x) es mayor que A.
En otras palabras, si para cualquier número positivo A que consideremos, existe un entorno reducido de a donde la función vale más que A, quiere decir que f(x) puede hacerse mayor que cualquier número, con tal de que x se acerque lo suficiente a a. Por eso se dice que el límite de f(x) cuando x tiende a a es +inf.

Caso 2:
limx->af(x) = -inf <=> para todo A > 0 existe δ > 0 / para todo x perteneciente al E*a,δ f(x) < -A .
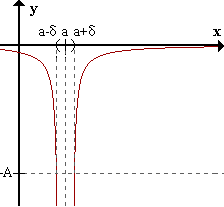
limx->af(x) = -inf <=> para todo A > 0 existe δ > 0 / para todo x perteneciente al E*a,δ f(x) < -A .

Caso 3:
limx->+inff(x) = +inf <=> para todo A > 0 existe B > 0 / para todox > B f(x) > A .
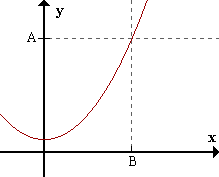
Para cualquier número positivo A (por grande que sea), es posible encontrar un número positivo B tal que para todos los x mayores que B, f(x) es mayor que A. Es decir que f(x) puede ser mayor que cualquier número, si x es lo suficientemente grande.
limx->+inff(x) = +inf <=> para todo A > 0 existe B > 0 / para todox > B f(x) > A .

Para cualquier número positivo A (por grande que sea), es posible encontrar un número positivo B tal que para todos los x mayores que B, f(x) es mayor que A. Es decir que f(x) puede ser mayor que cualquier número, si x es lo suficientemente grande.
Caso 4
limx->+inff(x) = -inf <=> para todo A > 0 existe B > 0 / para todox > B f(x) < -A .
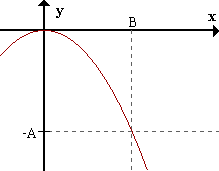
limx->+inff(x) = -inf <=> para todo A > 0 existe B > 0 / para todox > B f(x) < -A .

Caso 5:
limx->-inff(x) = +inf <=> para todo A > 0 existe B > 0 / para todox < -B f(x) > A .
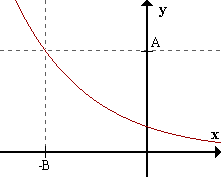
limx->-inff(x) = +inf <=> para todo A > 0 existe B > 0 / para todox < -B f(x) > A .
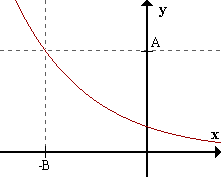
Caso 6:
limx->-inff(x) = -inf <=> para todo A > 0 existe B > 0 / para todox < -B f(x) < -A .
limx->-inff(x) = -inf <=> para todo A > 0 existe B > 0 / para todox < -B f(x) < -A .

Caso 7:
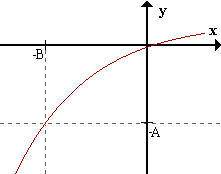
limx->+inff(x) = b <=> para todo ε > 0 existe B > 0 / para todox > B f(x) pertenece al Eb,ε.
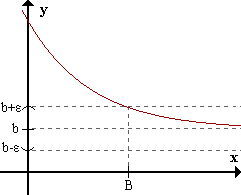
limx->+inff(x) = b <=> para todo ε > 0 existe B > 0 / para todox > B f(x) pertenece al Eb,ε.

Caso 8:
limx->-inff(x) = b <=> para todo ε > 0 existe B > 0 / para todox < -B f(x) pertenece al Eb,ε.
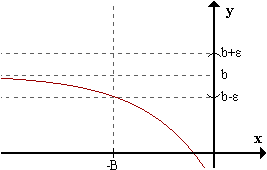
limx->-inff(x) = b <=> para todo ε > 0 existe B > 0 / para todox < -B f(x) pertenece al Eb,ε.

LIMITES INFINITESIMOS
Se dice que la función f es un infinitésimo cuando x → a, si se verifica 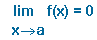




Es decir, un infinitésimo es una función cuyo límite es cero cuando la variable independiente x se aproxima hacia el valor x = a, o dicho de otra forma, una función cuyos valores se aproximan tanto más al cero cuanto más se aproxima x hacia el valor a.
Por tanto, en el concepto de infinitésimo hay que tener presente no sólo la función f, sino también el punto a. La función f es infinitésimo,en las proximidades del punto a. Suele decirse que es infinitésimo en x=a.
Para ciertos límites la regla de L'Hôpital no es aconsejable, pues la cantidad de veces en que ésta debe ser aplicada para llegar al resultado final se convierte en excesiva. Como ejemplo, el alumno puede tratar de hallar por L'Hôpital el límite:

límite que efectivamente puede ser hallado -pero tras un largo trabajo- mediante esta regla. Por el contrario, nuestro trabajo se simplifica notablemente si sustituimos en el denominador "sen x" por -lo que se llama infinitésimo equivalente-, "x". Entonces, el límite se reduce a:

A cuyo límite, transformado en más sencillo, podemos ahora aplicar la regla de L'Hôpital:
(aquí hemos utilizado la ralacion trigonometrica: sin(2x) = 2 sin x cos x ), llegamos al resultado final aplicando la regla de L'Hôpital otras tres veces más:
TEOREMAS RELATIVOS A INFINITESIMOS Y LIMITES.
TEOREMA
Dos infinitesimos son equivalentes <=> el orden de la diferencia es mayor que el orden de ambos.
H) f(x)x->a --->0, g(x)x->a--->0, f(x) equivalente g(x) cuando x->a
T) orden (f(x) - g(x)) > orden f(x)
orden (f(x) - g(x)) > orden g(x)
Demostración:
Directo:
1 1 pues f(x) equiv g(x)
--^-- --^-- x->a
f(x) - g(x) f(x) g(x)
lim ---------- = lim --- - --- = 0
x->a f(x) x->a f(x) f(x)
=> (por ordenes de infinitesimos) orden (f(x)-g(x)) > orden (f(x))
Análogamente se prueba que orden (f(x)-g(x)) > orden (g(x)).
Recíproco
orden(f(x) - g(x)) > orden (f(x)) => (por ordenes de infinitesimos)
f(x) - g(x)
lim ---------- = 0
x->a f(x)
1 (por def. infinitesimos equivalentes)
--^-- |
f(x) g(x) g(x) |
lim --- - --- = 0 => lim ---- = 1 => f(x) equiv g(x)
x->a f(x) f(x) x->a f(x) x->a
TEOREMA
La suma de dos infinitesimos de distinto orden es equivalente al infinitesimo de menor orden.
H) f(x)x->a --->0, g(x)x->a--->0 orden (f(x)) < orden (g(x)T) f(x) +g(x) equivalente a f(x) cuando x-<a.Demostración:1 0 pues orden (f(x)) < orden (g(x))--^-- --^-- f(x) + g(x) f(x) g(x) lim ---------- = lim --- + --- = 1 x->a f(x) x->a f(x) f(x)GENERALIZACION:La suma de n infinitesimos es equivalente al infinitesimo de menor orden.EJEMPLO: 7x5 + 4x3 + 2x2 equiv 2x2 cuan do x->0TEOREMASUSTITUCION DE INFINITESIMOS EQUIVALENTESH) limx->a α(x).f(x) = b (finito o infinito) α(x)x->a--> 0 Existe β(x), β(x)x->a--> 0 / β(x)x->a equiv α(x) T) limx-a β(x).f(x) = bDemostración:pues lim α(x)/β(x) = 1 | x->a α(x).β(x).f(x) | lim α(x).f(x) = lim --------------- = lim β(x).f(x) = b x->a x->a β(x) x->aTEOREMASUSTITUCION DE INFINITESIMOS EQUIVALENTESH) limx->a f(x)/α(x) = b (finito o infinito) α(x)x->a--> 0 Existe β(x), β(x)x->a--> 0 / β(x)x->a equiv α(x) T) limx-a f(x)/β(x) = bpues lim β(x)/α(x) = 1 | x->a f(x) β(x).f(x) | f(x) lim ---- = lim------------ = lim ---- = b x->a α(x) x->a β(x).α(x) x->a β(x)
domingo, 13 de octubre de 2013
Trabajo 1: DEFINICIONES DE FUNCION, DOMINIO, CONTRADOMINIO Y RANGO.
¿Que es una funcion?
Existen diferentes tipos de expresiones algebraicas, sin embargo algunas de las expresiones que mas nos interesa dentro del cálculo son las funciones.
Una función es una regla de asociación que relaciona dos o mas conjuntos entre si; generalmente cuando tenemos la asociación dos conjuntos las función se define como una regla de asociación entre un conjunto llamado dominio con uno llamado codominio, también dominio e imagen respectivamente o dominio y rango. Esta regla de asociación no permite relacionar un mismo elemento del dominio con dos elementos del codominio.
¿Que es el dominio?
En matemáticas, el dominio (conjunto de definición o conjunto de partida) de una función f \colon X \to Y \, es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota \operatorname{Dom}_f\, o bien D_f\,. En \R^n se denomina dominio a un conjunto conexo, abierto y cuyo interior no sea vacío.
Por otra parte, el conjunto de todos los resultados posibles de una función dada se denomina imagen de esa función.

¿Que es el contradominio, codominio o rango?
El otro conjunto que interviene en la definición es el conjunto llamado codominio o rango de la función, en ocasiones llamado imagen, este conjunto es la gama de valores que puede tomar la función; en el caso del plano son todos los valores que puede tomar la función o valores en el eje de las Y´s.
También, cuando se grafica en el plano cartesiano se tiene una relación de dos variables, considerando como variable aquella literal que esta sujeta a los valores que puede tomar la otra.
Trabajo 2: TIPOS DE FUNCIONES.
TIPOS DE FUNCIONES.

FUNCIONES POLINOMICAS
FUNCIÓN LINEAL
Es una función de la forma f(x) = mx + b, donde m es la pendiente y b es la abscisa donde la recta intercepta al eje. La grafica que se origina es una línea recta, si m es positiva la recta se inclina hacia la derecha y si m es negativa la recta se inclina hacia la izquierda.
EJEMPLO:
FUNCIÓN CONSTANTE
Es una función de la forma f(x) = k, donde k es una constante. La grafica que se origina es una línea recta paralela al eje x.
El dominio de la función constante son todos los números reales y el rango es un conjunto unitario formado por el elemento imagen de todos los elementos del dominio.
EJEMPLO:
EJEMPLO:
Ø FUNCIÓN
Es una función de la forma f(x) = ax2+ bx +c, donde a,b,c y son números reales. La grafica de la función cuadrática es una curva llamada parábola; si a es positiva, la grafica abre hacia arriba y si a es negativa la grafica abre hacia abajo.
La ecuación algebraica tiene el 2 como máximo exponente de la variable.
EJEMPLO:
FUNCIÓN POLINOMICA
Una función Polinómica es de la forma f(x) = anxn+an-1xn-1+…+a donde an,an-1,…,a son constantes reales y n es numero entero no negativo que indica el grado de p(x), siempre que an≠0.
Ejemplo:
Ø
FUNCIONES ESPECIALES
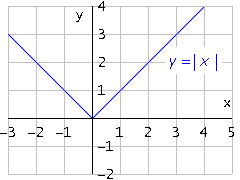
FUNCIÓN VALOR ABSOLUTO
FUNCIONES ESPECIALES
FUNCIÓN VALOR ABSOLUTO
La función valor absoluto se define como:
Es de la forma f(x) = IxI, cuyo dominio son los reales y el rango son los reales mayores o iguales a cero. La grafica que se obtiene es una curva en forma de v.
EJEMPLO:
Ø
Ø FUNCIÒN RAIZ CUADRADA
Es una función que asigna a un argumento su raíz cuadrada positiva. Es de la forma f(x) = √x , donde el dominio de la función son los valores de x que hacen que el radicando sea positivo y el rango son los reales mayores o iguales a cero. La grafica que se obtiene es una curva ascendente que está por encima del eje x
Ejemplo:
Ø FUNCiÓN RACIONAL
Es una función de la forma f(x) = p(x)/q(x) , donde p(x) y q(x) son polinomios y q(x)≠0. La función racional no está definida para valores de x en el cual q(x) se hace diferente de cero, este valor al representarlo gráficamente es una asíntota. La grafica que se obtiene son curvas interrumpidas por la asíntota.
Ejemplo:
Ø FUNCIONES TRASCENDENTALES
FUNCIÓN EXPONENCIAL
FUNCIÓN EXPONENCIAL
Es una función de la forma f(x) = ax, donde a>o y a≠1 .cuyo dominio son los números reales y el rango son los reales mayores que cero. La grafica que se obtiene es una curva ascendente si a>1 y descendente si o<a<1.
Ejemplos:

Ø FUNCIÓN
Es una función inversa a la función exponencial, es de la forma
f(x) = logax, donde a>o y a≠1. La grafica que se obtiene es una curva simétrica a la función exponencial.
f(x) = logax, donde a>o y a≠1. La grafica que se obtiene es una curva simétrica a la función exponencial.
Ejemplos:
Ø FUNCIÓN
Las funciones trigonométricas surgen de estudiar el triangulo rectángulo y observar que las razones (cocientes) entre las longitudes de dos lados cualesquiera dependen del valor de los ángulos del triangulo. Se distinguen seis tipos de funciones trigonométricas, Las cuales cada una de ellas tiene su dominio, rango, periodo y su gráfica es distinta, como son:
Ejemplos:
f(x) = sen x
f(x) = sen x
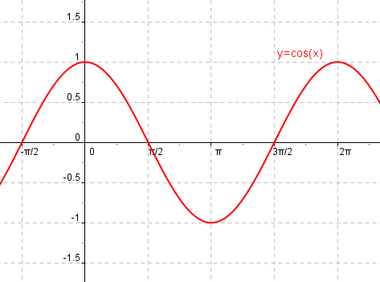
f(x) = cos x
f(x) = tan x
f(x) = cot x
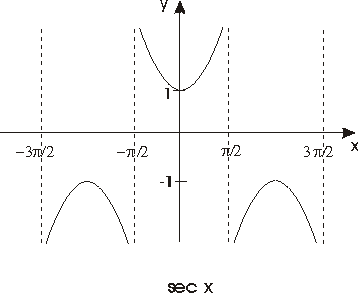
f(x) = sec x
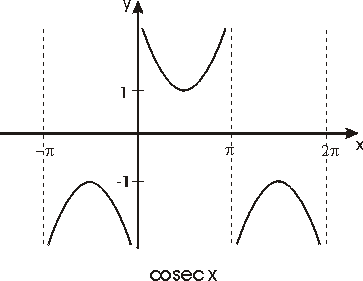
f(x) = cscx
Suscribirse a:
Comentarios (Atom)