Observemos la función f(x)=1/x2 para valores de x positivos muy grandes.
| x | f(x) |
|---|---|
| 100 | 1,0x10-4 |
| 1.000 | 1,0x10-6 |
| 10.000 | 1,0x10-8 |
| 100.000 | 1,0x10-10 |
| 1.000.000 | 1,0x10-12 |
Si tomamos x cada vez mayor, f(x) está cada vez más cerca de 0. Si x es suficientemente grande podemos conseguir que f(x) se acerque a 0 tanto como queramos. Decimos que f(x) tiende a 0 cuando x tiende a infinito.
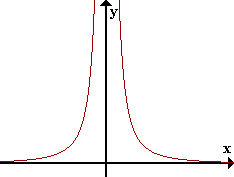
Veamos a continuación las definiciones precisas de cada uno de los límites que involucran al infinito.
PROPIEDADES.
Caso 1:
limx->af(x) = +inf <=> para todo A > 0 existe δ > 0 / para todo x perteneciente al E*a,δ f(x) > A .
El límite de f(x) cuando x->a es infinito positivo, si para cualquier número positivo A (tan grande como se quiera), podemos encontrar un número δ tal que, para todos los x dentro del entorno reducido de a de radio δ se cumple que f(x) es mayor que A.
En otras palabras, si para cualquier número positivo A que consideremos, existe un entorno reducido de a donde la función vale más que A, quiere decir que f(x) puede hacerse mayor que cualquier número, con tal de que x se acerque lo suficiente a a. Por eso se dice que el límite de f(x) cuando x tiende a a es +inf.
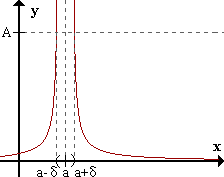
limx->af(x) = +inf <=> para todo A > 0 existe δ > 0 / para todo x perteneciente al E*a,δ f(x) > A .
El límite de f(x) cuando x->a es infinito positivo, si para cualquier número positivo A (tan grande como se quiera), podemos encontrar un número δ tal que, para todos los x dentro del entorno reducido de a de radio δ se cumple que f(x) es mayor que A.
En otras palabras, si para cualquier número positivo A que consideremos, existe un entorno reducido de a donde la función vale más que A, quiere decir que f(x) puede hacerse mayor que cualquier número, con tal de que x se acerque lo suficiente a a. Por eso se dice que el límite de f(x) cuando x tiende a a es +inf.

Caso 2:
limx->af(x) = -inf <=> para todo A > 0 existe δ > 0 / para todo x perteneciente al E*a,δ f(x) < -A .
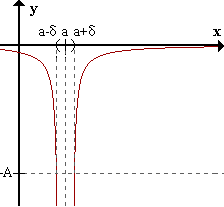
limx->af(x) = -inf <=> para todo A > 0 existe δ > 0 / para todo x perteneciente al E*a,δ f(x) < -A .

Caso 3:
limx->+inff(x) = +inf <=> para todo A > 0 existe B > 0 / para todox > B f(x) > A .
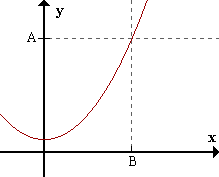
Para cualquier número positivo A (por grande que sea), es posible encontrar un número positivo B tal que para todos los x mayores que B, f(x) es mayor que A. Es decir que f(x) puede ser mayor que cualquier número, si x es lo suficientemente grande.
limx->+inff(x) = +inf <=> para todo A > 0 existe B > 0 / para todox > B f(x) > A .

Para cualquier número positivo A (por grande que sea), es posible encontrar un número positivo B tal que para todos los x mayores que B, f(x) es mayor que A. Es decir que f(x) puede ser mayor que cualquier número, si x es lo suficientemente grande.
Caso 4
limx->+inff(x) = -inf <=> para todo A > 0 existe B > 0 / para todox > B f(x) < -A .
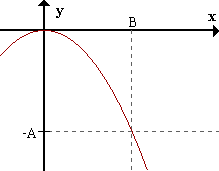
limx->+inff(x) = -inf <=> para todo A > 0 existe B > 0 / para todox > B f(x) < -A .

Caso 5:
limx->-inff(x) = +inf <=> para todo A > 0 existe B > 0 / para todox < -B f(x) > A .
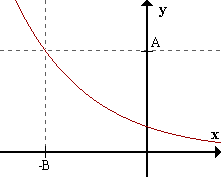
limx->-inff(x) = +inf <=> para todo A > 0 existe B > 0 / para todox < -B f(x) > A .
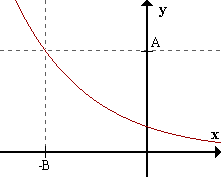
Caso 6:
limx->-inff(x) = -inf <=> para todo A > 0 existe B > 0 / para todox < -B f(x) < -A .
limx->-inff(x) = -inf <=> para todo A > 0 existe B > 0 / para todox < -B f(x) < -A .

Caso 7:
limx->+inff(x) = b <=> para todo ε > 0 existe B > 0 / para todox > B f(x) pertenece al Eb,ε.
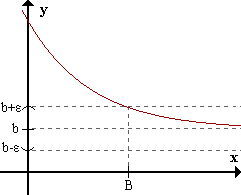
limx->+inff(x) = b <=> para todo ε > 0 existe B > 0 / para todox > B f(x) pertenece al Eb,ε.

Caso 8:
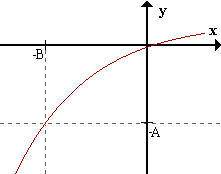
limx->-inff(x) = b <=> para todo ε > 0 existe B > 0 / para todox < -B f(x) pertenece al Eb,ε.
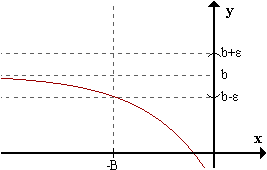
limx->-inff(x) = b <=> para todo ε > 0 existe B > 0 / para todox < -B f(x) pertenece al Eb,ε.

No hay comentarios.:
Publicar un comentario